| Главная » Статьи » Структуры |
СТРУКТУРЫ ч. II
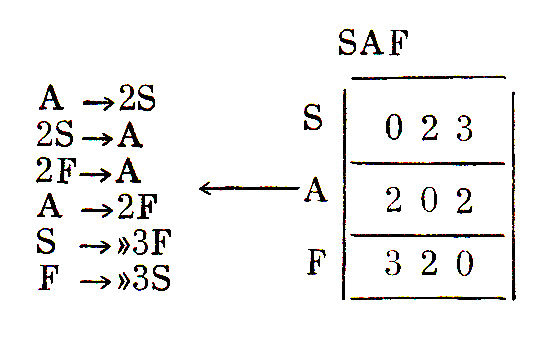
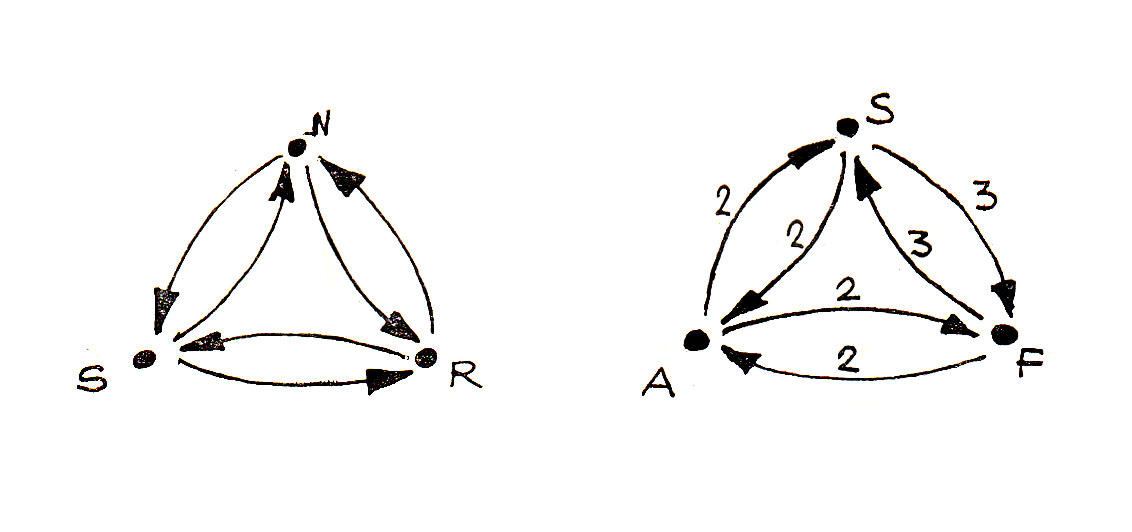
АВТОР ДАВИД ЖОРЖ ЭММЕРИХ (DAVID GEORGES EMMERICH)С тех пор как сопротивление материалов заняло место строительной науки, конструкции стали классифицировать произвольно, по материалу: дерево, камень, сталь, бетон..., тогда как сущность конструкций прежде всего геометрическая, или, в более широком смысле, морфологическая, а следовательно, поведение конструкций не зависит от физического характера ее составляющих. Например, цепь может быть составлена из стальных колец высокой прочности, но при этом она останется деформируемой конструкцией, степень свободы которой ограничена ее способностью вытянуться в прямую линию. Можно, конечно, приварить кольца друг к другу, но тогда будет потерян характер цепи. И, наоборот, тетраэдр рассматривается как устойчивая структура, даже если он будет выполнен из соломы, поскольку его элементы лишены возможности движения и занимают взаимно определенное геометрическое, жесткое, следовательно, статичное положение. Таким образом, поскольку судить о конструкциях можно только по их виду, следует их классифицировать прежде всего по пространственным или топологическим признакам. Но сначала следует вернуться к различию, существующему между формой и структурой. В общем, топологическом смысле формой называется сумма постоянных и временных свойств любого явления или живого существа. Сумма неизменных свойств образует структуру, а сумма потенциальных и изменяемых свойств — ее возможности. Форма, в специфическом смысле этого слова, только одно из состояний общей формы, содержащей все состояния. Форма, не допускающая никаких изменений, лишена какой-либо степени свободы, т. е. статична; если форма обладает ограниченной свободой, т. е. только один или несколько ее элементов регулируются, а ее деформация поддается контролю, то речь идет о механизме; если движение нельзя координировать, говорят об «аморфной» или непрочной форме. Понятие прочности, твердости, жесткости или вязкости в молекулярном масштабе связано с основной структурой материалов. Несмотря на существующую аналогию между прочностью материалов и несущих конструкций, здесь существует разрыв масштаба, исключающий всякое смешение индивидуального сопротивления составляющих и общей устойчивости структуры в целом. Структура не является по своему определению чем-то единым и монолитным, в то же время, если она состоит из нескольких частей, ее нельзя считать просто суммой ряда материалов; ее существо заключается в расположении и природе ее членений, даже в последовательности положений, занимаемых отдельными частями в ходе строительства этой головоломки. Здесь мы имеем дело с отдельными частями и способом их применения, как в языке со словами и синтаксисом. Когда мы подходим к структуре как к объекту проектирования, трудность заключается в организации многочисленных данных, т. е. в определении связей между составляющими ее элементами. Чтобы понять сущность формы, ее конструктивную схему, ее структуру, следует определить законы, в соответствии с которыми устанавливается координация ее элементов, и зафиксировать их взаимное расположение — их распределение. Так, для конструирования формы недостаточно вывести сумму или составить перечень элементов, тем более что не все они одинаковы. Какова бы ни была природа структуры, в ней всегда можно выделить три типа элементов: узлы, соединительные стержни и зоны. Эти три основные топологические единицы являются естественным членением пространства или среды, в которой размещена структура. Узел играет здесь роль локализатора; соединительный стержень является разделителем и одновременно связью; зона определяет деление на участки. Соединенные между собой в определенном порядке их размещения, эти единицы образуют линейные, плоскостные, пространственные и сверхпространственные формы. Именно эта сумма направлений, или связей между элементами, определяет постоянные особенности данной формы, схематически организованной в виде трех деталей, состоящих из двух одинаковых частей. Под понятием «структура» подразумевается ансамбль, состоящий из узлов, соединительных стержней и зон (хотя бы по одному), композиция которых удовлетворяет следующим условиям: Эту схему можно изобразить в виде фигуры, в которой все связи имеют вид ориентированных арок, а ее сущность определяют вершины. Полученное графическое изображение с тремя вершинами, шестью стержнями и пятью зонами является главным структурным элементом всей структуры. Вышеуказанные минимально необходимые свойства, перечисленные в отношении этих трех пар, могут быть отнесены к расширенной схеме путем замены формулировки — «один или несколько». Так, например, термин «то же число» в каждой фразе определяет строгую правильность структуры. По-видимому, между общей первой схемой и точно соответствующей последней расположено бесконечное число структур самой различной сложности и правильности. В самом деле, элементы ситуации или определители нашей комбинационной машины могут получать такие ограничительные указания, как «только», «по меньшей мере»..., или даже точные цифровые величины «один», «два», «три»... Выбор серии — в принципе свободный при условии, что она не противоречива, впрочем, без этого любой выбор будет случайным. В качестве примера возьмем определение трех пар, имеющих свойства того класса структур, которые носят название выпуклых многогранников и соответствуют теореме Штейница (Steinitz). Это будет выглядеть следующим образом: 1а — каждое ребро связано только с двумя вершинами; Все это можно записать в виде упрощенного алгебраического выражения, изобразить в графике или в виде таблицы, одинаково читаемой с начала и с конца так называемой (double entree) «матрицы связей»:
Из этих изображений видно, что элемент не может быть связан с самим собой и что он существует только благодаря связи по меньшей мере с двумя элементами другого типа. Следует также отметить, что топологические термины NSR заменены соответствующими им в простом геометрическом пространстве терминами SAF. Тем не менее существуют более сложные пространства, где роль Узла, Соединительного стержня и Зоны играет триада Угол, Грань и Многогранник или в пространстве высшего измерения — Грань, Многогранник и Сеть и т. д. Так, размерность пространственной структуры определяется положением трех последовательных терминов в ряду: SAFPR1R2....... Еn_3, Еn_2, En_1. где первые три характеризуют выпуклое пространство, наименее сложное, а три последних n — размерное пространство Еn.
Теперь можно кратно перечислить в порядке возрастающей сложности различные группы форм: выпуклые тела и подобные им — цепи, многоугольники, деревья, лабиринты, сетки, многогранники..., кольцеобразные формы и другие поверхности второго порядка и им подобные узлы, переплетения, плетения, ткани...; далее тела и системы с количеством измерений n и вытекающие из них все возможные бесчисленные изменения форм. Таким образом, исходя из наиболее общих типов и в дальнейшем ограничиваясь правильными и повторяющимися элементами, мы приходим к установлению широкого набора форм, которые можно практически неограниченно развивать, расширять и комбинировать. Но этот перечень, абстрактно построенный и постепенно усложняющийся в соответствии с логическим методом, основанным на непрерывности возможного движения в пространстве, если он и содержит неисчерпаемые богатства доступных воображению форм, то не всегда может быть конкретно материализован с сохранением всех преимуществ при практическом воплощении. При этой совершенно формалистической игре воображения из разных видов форм, реализованных в равных условиях, одни будут достаточно устойчивыми, другие нет. По-видимому, из бесконечного числа геометрических структур следует выбирать только годные для строительства, в противном случае, при отсутствии устойчивой формы, т. е. такой формы, которая сохраняется на подвешенных соединениях, здание потеряет эту форму, превратится в бесформенную массу, будет напоминать работу троглодитов, прорезывающих отверстия в блоке, что в наше время выглядит смешно. В каждом морфологическом классе существуют избранные, от природы устойчивые формы, такие как: треугольники, дельтоэдры, компактные сочетания, естественно притягивающее архитекторов. В каждом (классе существуют один или несколько идеально правильных видов; таковыми являются прямая линия, устойчивый шахматный порядок, не имеющие практического значения сочетания, и другие менее правильные, но реже или чаще повторяющиеся системы. Повторяемость — чрезвычайно ценное свойство при серийном изготовлении элементов. Кроме того, определенные элементы могут войти в композицию целого ряда структур, так как по своим комбинационным свойствам эти элементы, подобно универсальному кирпичу, создают настоящую конструктивную игру. И наконец, для иллюстрации размаха этой структурной типологии, охватывающей даже человеческое мышление, следует сказать, что в принципе все идеологии могут быть выражены прямой или даже кривой, а методологические, так называемые правильные структуры, стремятся к форме дерева. Физики уже имеют дело с пространствами, исчисляющимися миллионами километров. Следует отметить, что архитектура все еще сводится к такой топологически плоской и в высшей степени неустойчивой форме, как куб. Большая часть строящихся в настоящее время структур имеет форму призмы с прямоугольным основанием; вертикальным ограждением и горизонтальным планом. Такие элементы, если они не отлиты целиком, с точки зрения законов статики бесполезны один для другого. Это, несомненно, чрезвычайно примитивная манера, примеры применения которой можно найти в древности; такова могила Теодориха в Равенне, возведенная доисторическими методами, как дольмены. Чтобы лучше оценивать эту технику и причины ее живучести, следует вспомнить, что примитивный человек был троглодитом, т. е. жил в дыре, проделанной в любой массе. Когда, набравшись некоторых знаний, человек начал строить, ему потребовалось время, чтобы понять, что нужна только дыра, а не окружающая ее масса. Но еще долго он пользовался примитивной техникой, державшей его под тяжелым игом, по существу бесполезной массы. По контрасту с этим, одновременно разобщенным и монолитным методом строительства своды и купола, по природе своей составные, являются соединениями, части которых, взятые изолированно, рушатся без совместной со всеми другими элементами работы. Из этой их особенности вытекает известная экономия материалов, т. е. массы. Каковы бы ни были объяснения, относящиеся к истории происхождения куполов, характер совместной работы их составляющих твердо установлен. По мнению одних их можно рассматривать как кольцевые стены, верхние слои которых, соскальзывая, сближались и, соединяясь друг с другом, образовывали коническую оболочку, подобную греческим куполообразным кровлям, наиболее известным примером которой является верхняя часть сокровищницы Атрея. По мнению других эта конструктивная форма происходит от соединения длинных, заглубленных в землю мачт, верхние концы которых были изогнуты и связаны между собой.
Могила короля Теодориха 520 г., Италия. Пантеон Агриппы 126 г. Рим. Какие бы ни выдвигались объяснения, происходят ли купола от систем, работающих на сжатие или на растяжение, суть заключается в солидаризации множества элементов для получения центрированной или кольцевой композиции, устойчивость которой значительно превосходит линейные соединения, где элементы просто соединены друг с другом или наложены один на другой без какого-либо объединения их рабочих усилий, т. е. без возможности сплотиться и консолидироваться. Во всяком случае не подлежит сомнению, что центрированные сооружения были изобретены раньше линейных. Часто бывает, что развитие вспомогательной техники, например открытие изотропных высокопрочных материалов, вместо того чтобы связать достоинства материалов с формой, с самого начала способствует использованию менее рациональной формы и тем самым ограничивает общую техническую эволюцию. В общем виде формы, охватывающие простое пространство, классифицируются в соответствии с образующими их поверхность кривыми. По своему внешнему виду эти кривые делятся на три вида: вогнутые, прямые и выпуклые. Статическое поведение структуры определяется именно этими геометрическими данными: в таких вогнутых формах, как катеноиды, преобладает растяжение, следовательно, это натянутые конструкции; в случае прямолинейных форм, таких как плоские плиты, возникают усилия растяжения и сжатия, т. е. это конструкции, работающие на изгиб; и, наконец, в выпуклых формах, за исключением пневматических конструкций, являющихся своего рода троглодитизмом, где воздух заменяет массу, преобладают усилия на сжатие. Существуют и сложные, более развитые структуры двоякой кривизны, такие как гиперболические параболоиды и другие поверхности, в которых перемежаются растяжение и сжатие в чистом виде, или другие формы со сложными усилиями, изгибом и кручением различной ориентировки, поэтому предложенную нами классификацию форм следует считать упрощенной. Выпуклые формы вызывают центробежные усилия, действующие на опоры, тогда как вогнутые формы вызывают концентрическое кручение, требующее заанкеривания, часто более дорогостоящего, чем сами опоры. У плоских плит возникают только вертикальные реакции. Такие плиты могут быть просто уложены на опоры, чем частично и объясняется их широкое распространение. Этим же свойством обладают некоторые составные самонесущие и самонатянутые конструкции, не передающие никаких усилий на опоры. Следует еще отметить, что, как правило, вогнутые и плоские сооружения требуют дополнения в виде стен, тогда как преимуществом куполов является их способность образовывать замкнутые объемы, не требующие никаких дополнительных ограждений. Римские купола, в частности пантеон Агриппы диаметром 44 м, были выпуклыми конструкциями со сжатыми элементами. Иначе не могло и быть, поскольку камень, хрупкий от природы, практически не работает на растяжение. Камни в основном были связаны весом. Чтобы использовать это свойство, которым в достаточной мере обладали тесаные камни, приходилось укладывать их в положение неравновесия. Сумма возникающих давлений одного камня на другой создавала более высокое равновесие, чем сумма неравновесий. Принцип был простой: камни обтесывали таким образом, чтобы они были смещены по вертикали, обычно путем стески наклонных поверхностей, перпендикулярных изгибу свода. Но чтобы это сделать, приходилось измерять, делить, стесывать,.., и совершенно очевидно, что в основе этой техники лежала та же геометрия. И действительно, на протяжении длительных периодов истории строительное искусство и стереометрия были слиты воедино. В процессе применения примитивных конических форм быстро замечены преимущества сферических сводов, где почти отсутствуют горизонтальные усилия, поскольку нагрузки передаются по вертикали на основание. Стремясь использовать эти преимущества, купол стали поднимать на барабан или придавать ему овоидальную форму, в эпоху возрождения вернулись хотя и к ребристому, но все же сферическому или разделенному на части, как парашют, куполу. Барокко принесло с собой пониженную и более плоскую форму арки в виде эллипсоида, арки с двумя центрами и даже более сложные пространственные кривые сводов. В ходе эволюции средства для выражения этой формы усложнялись и обогащались. Уже в полусферическом куполе пантеона были применены пространственные разгрузочные арки двоякой кривизны. Косые оболочки в капелле Пацци во Флоренции могут служить моделью для тонких бетонных оболочек. Их автор Брунеллески не отступил перед строительством двойного ребристого свода в куполе собора во Флоренции диаметром 46 м, высотой 100 м. Позднее стали появляться умелые интерпретации поверхностей вращения, которые можно встретить в церкви Сан-Лоренцо в Турине, построенной Гварини, или в сооружениях Бальтазара Неймана в Франконии. Совершенно очевидно, что эволюция архитектурных форм проходила параллельно с обогащением геометрических познаний, а реальное строительство следовало почти сразу за теоретическим выявлением новых форм.
Сокровищница Атрея 1250 г. до н. э. Греция. Капелла Пацци 1443 г. Если рассматривать другой материал более отдаленных эпох — дерево, то здесь, за редким исключением, мы также обнаружим неизбежное присутствие геометрии, хотя ее применение в этой области сведено к плоскости. Причины этого ограничения заложены в природе самого дерева — материала, работающего только по длине на сжатие и растяжение, промышленная обработка которого сводилась к распиловке. Преобладание прямоугольных планов, в лучшем случае покрытых треугольными фермами, вытекает из применения таких материалов, как доски и брусья. Деревянные сооружения до нашего времени сохранили свой плоский, составной, вытянутый в длину характер. Концентрические деревянные сооружения встречаются сравнительно редко, за исключением некоторых славянских районов, где в культовых зданиях сохранилось византийское влияние, и в надстройках колоколен. Но, независимо от назначения этих деревянных зданий, конструкции их перекрытий всегда сохраняют характер ферм, хотя в отдельных случаях фермы не устанавливаются рядами, а пересекаются, образуя пирамиду или конус. По этому методу была построена большая часть куполов периода классицизма, в том числе купол собора Св. Павла в Лондоне, где несущие конструкции имеют форму пучка прямых балок, а наружные и внутренние контуры образованы дополнительными габаритами из досок. На деле эти пакеты, независимо от наклона образующих, представляют собой просто ложные купола. Большим недостатком таких форм следует считать то обстоятельство, что при радиальной конфигурации, где число элементов идентично на периферии и в центре, диаграмма усилий не соответствует форме. При постоянном числе отрезков усилия в них различные: в основании, где сосредоточиваются нагрузки, элементы расположены с большими интервалами, тогда как в вершине, где усилия почти отсутствуют, образуется бесполезное скопление отрезков, кроме всего прочего затрудняющее сборку. Этим основным противоречием объясняется малое распространение и развитие сооружений такого рода. Несмотря на свойственные центрированным формам достоинства, круглых деревянных зданий мало, и только фермы, все увеличиваясь по длине, перекрывали пррлеты до 50 м, как в Московском манеже. В свете этих исторических прецедентов становятся более понятными формы промышленного века, где сначала преобладали металлические конструкции. За исключением короткого периода, когда использовали литое железо, т. е. чугун, эти конструкции, как правило, сооружались из длинных продолговатых полос, полученных не распиловкой, а прокаткой. Принятые же для металла профили по инерции повторяли старый материал — дерево. Металлы сохраняли ортогональные профили: листовое железо, рельсы, уголки и т. д. и только заменяли доски, стропила, бруски и пр. Использовать в строительстве трубы начали сравнительно недавно. Совершенно естественно, что металлические профили, копировавшие дерево, использовались в конструкциях, подобных деревянным, и это несмотря на то, что формы были неоправданными, а металл как изотропный материал работал так же хорошо, если не лучше, на растяжение, как и на сжатие, одинаково во всех направлениях; он достаточно гибок для изготовления ориентируемых во всех направлениях профилей и соединений. Отныне стало возможным монтировать настоящие несущие механизмы, невыполнимые из дерева и камня. Но еще в течение длительного времени металл не мог найти присущий ему язык форм, в которых бы отразились его предельные возможности. Широко распространившиеся с XIX века металлические купола повторяли конструкции деревянных с их радиоконцентрической композицией и перпендикулярно соединенными элементами. Насколько нам известно, это правило не имеет исключений, если не считать аудитории Гимар (Guimard), растительного стиля на улице Сан-Дидье, в настоящее время разрушенной, и неосуществленных проектов Виолле ле Дюка. Здание Национальной библиотеки в Париже Лабруста, галереи Милана Менгони, купол Капитолия в Вашингтоне и даже большая часть современных куполов страдают тем же недостатком: несущие элементы собраны в вершине, где они не нужны, и разрежены в основании, где их не хватает. Такое разрежение элементов изредка исправлялось не радиальным, а централизованным, геометрическим их распределением. Одни делили купол на концентрические кольца из треугольников по системе Шведлера, другие вдохновлялись капеллой Ане Филибера Делорма, заменяя прямые радиальные элементы двумя рядами пересекающихся спиралей. Все эти улучшения только уменьшали основное расхождение между централизованной формой и центробежными усилиями. | |
| Категория: Структуры | |
| Просмотров: 2665 |